Whitepaper: SystemC AMS Extensions—Solving the Need for Speed
By Martin Barnasconi, AMS Working Group Chairman, Open SystemC Initiative
May 2010
Abstract—In March 2010, the Open SystemC™ Initiative (OSCI) released the SystemC Analog/Mixed-signal (AMS) 1.0 standard, introducing AMS language constructs and semantics as natural extensions to SystemC. This new standard fulfills the need for a unified system-level modeling language to design and verify real heterogeneous applications composed of AMS and digital HW/SW systems. In addition, it allows modeling at higher levels of abstraction, which significantly improves the simulation performance (speed) and efficiency.
Similar to Transaction-level Modeling (TLM), the SystemC AMS extensions introduce smart methods to abstract time and uses known techniques to abstract signal properties. However, analog behavior is continuous in time and continuous in value, captured in an equation system and often seen as difficult to abstract. Any abstraction method applied would result in a less accurate description of the analog behavior. This is not necessarily a problem, as long as the abstracted behavior does not impact the essential characteristics or functionality of the AMS system for the intended application. So, when applying these abstraction methods in a smart manner, a major improvement in simulation speed is obtained, enabling totally new AMS analysis and verification methods through simulation, which have never been exercised before.
I. SystemC AMS in Virtual Prototyping: The Missing Link
Virtual prototyping is a well known technique applied in digitally-oriented ESL design methodologies. The objective is to create a reference platform of the complete system or IC architecture (the "prototype" part) in an executable description captured in an abstract model (the "virtual" part), which is then simulated. In this way, virtual prototyping provides software developers and system architects with an environment for software development, architecture exploration, or HW/SW co-design.
However, virtual prototypes based on purely digital models and model descriptions may not offer an efficient way to capture analog behavior, which is often an integral part of the embedded system. This can be a serious drawback, as the interfaces to the outside world – which are analog in nature – are thus not adequately modeled or even not modeled at all. Examples of these analog interfaces are sensors and actuators, wireless or wired physical layer (PHY) blocks of a communication system, or the power supply and management unit of an integrated circuit. Furthermore, for optimized system architectures containing analog, digital, and software functionality, the software or firmware often directly interacts with AMS hardware. Therefore, the correctness and robustness of the system in terms of its architecture, functional aspects, and timing aspects cannot be validated in the analog or digital domain only, and mixed-signal simulations may be needed.
The biggest constraint of introducing AMS descriptions in a virtual prototype is that they should not result in degradation of the simulation speed. For example, this can be an issue with mixed-signal simulation if the AMS description is at the wrong level of abstraction. They should offer sufficient accuracy to describe the (abstracted) analog behavior for the intended use case [1]. For this reason AMS descriptions at a high level of abstraction are more suitable to combine AMS subsystems with HW/SW subsystems in a virtual prototype.
II. SystemC AMS Abstractions: The Art of Simplification
SystemC AMS extensions introduce three different models of computation to support AMS behavioral modeling at different levels of abstraction. These models of computation are Electrical Linear Networks (ELN), Linear Signal Flow (LSF), and Timed Data Flow (TDF). ELN and LSF descriptions are used to model continuous-time behavior, for which simulations only require a simple linear analog solver. TDF descriptions are processed at discrete points in time. As depicted in Table 1, four abstraction methods can be applied for each model of computation:
- abstraction of the behavior
- abstraction of the structure
- abstraction of the communication
- abstraction of the time and frequency
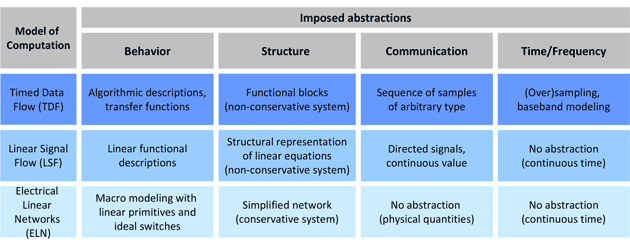
Table 1: Abstractions in relation to the SystemC AMS models of computation [2].
Abstraction of the behavior will change the actual functionality of a representation, as it focuses on what and what not to model. Behavioral abstraction is often seen as difficult, due to the fact that the criteria to decide what can or cannot be left out of a behavioral description are highly application-specific and use-case dependent. This requires some thinking (and specification) from the AMS designer together with the architect to evaluate and define the relevant functionality only, which is then captured in a behavioral model.
Abstraction of the behavior can be applied at different structural levels and using different formats. In case of an electrical network, macro modeling is applied. Macro modeling uses electrical primitives to replace the physical representation with an ideal equivalent circuit. Behavioral abstraction applied to blocks (such as amplifiers) may use a Laplace transfer function with poles and zeros to capture the dynamic linear behavior, or could be replaced by an abstract static non-linear description in a TDF model. A behavioral abstraction of a look-up table means that the table is further condensed.
Abstraction of the structure is the most obvious method used to simplify the composition and thus architecture of a design, without changing its behavior. It decouples the implementation details (how it is modeled) from the actual functional description (what is modeled). It describes the system in (a set of) models, where for each model the outputs are defined as a function of the inputs.
This method heavily influences the granularity of the system, which could impact the simulation performance. Especially when using electrical primitives, the number of models used will define the size of the overall equation system. It is expected that a fine-grained description will result in reduced simulation speed compared to a course-grained description.
The need for a particular level of structural detail strongly depends on the system properties or characteristics being specified or analyzed. For example, in case the value of an electrical component needs to be defined, a network of electrical primitives needs to be resolved with an analog solver, taking into account the conservative behavior of the electrical network. As soon as the system can be partitioned using independent entities, each defining a specific functionality, a non-conservative system description using directed signals is sufficient. This will help to speed up simulations.
Abstraction of the communication allows the use of different data types to abstract the signals used for communication. Figure 1 provides an example of different abstraction methods for analog signals related to the model of computation used (see also Table 1). Although for completeness the signal amplitude as function of time is depicted, the relevant element for this abstraction method is the amplitude value of the signal.
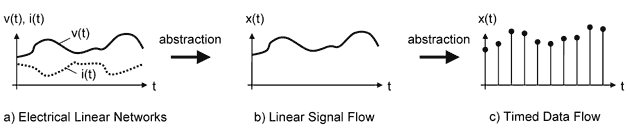
Figure 1: Abstraction of communication and time using the SystemC AMS models of computation.
For conservative system descriptions (such as electrical networks) there are two dependent quantities: the voltage v(t) at each node (known as the across value) and the current i(t) through each electrical primitive. An equation solver has to calculate all across values (voltages) and all through values (currents) in a way that the Kirchhoff's Laws are fulfilled. For signal flow and data flow descriptions, which describe the network as a nonconservative system, no such dependency exists between these quantities. A single quantity x(t) is used, which then represents, for example, either the voltage or the current.
For electrical networks and signal flow descriptions, the analog signal representation is continuous in value and time. No data type is available in the SystemC AMS extensions to provide direct access to this value, due to the fact that this signal is an integral part of the analog equation system. For Timed Data Flow, the values of the signal representation are available at discrete points in time and may use any arbitrary data type to represent the signal value. For example, the data type double can be used to represent a continuous value for the amplitude of the signal.
Abstraction of time and frequency is the most powerful—but also the most tricky—part of the SystemC AMS extensions. This seems impossible for analog signals, as the continuous-time property of a signal is a fundamental part of the analog description. However, such an abstraction method is extremely useful to improve efficiency in AMS system-level modeling. In fact, concepts similar to those applied to TLM have been introduced for AMS, enabling the abstraction of time.
The first method is to apply (over)sampling to the analog signal, resulting in a discrete-time sampled signal. The main advantage of using the TDF model of computation is that the sampled values are processed efficiently. Time annotation ("tagging") is applied to define the exact time stamp for each sample. Note that this sampling technique should be applied with care. When dealing with radio frequency (RF) signals, the sampled discrete-time signal should comply with the Nyquist-Shannon Sampling Theorem, which defines that the signal is preserved when it is sampled with at least the Nyquist frequency, being at least twice the maximum signal frequency. In order to apply this method on analog signals and to avoid aliasing, a sufficiently high oversampling ratio is needed.
When modeling RF systems with very high carrier frequencies (in the order of GHz), a significant simulation speedup can be achieved by applying abstraction of the frequency, known as baseband modeling. This second abstraction method is based on the fact that digital modulation techniques used in modern communication systems use the amplitude and the phase of the analog signal to transmit information. In this case the information itself is independent from the (usually high) carrier frequency. The idea of baseband modeling is to map the RF carrier frequency to zero hertz. The resulting signal is called the complex lowpass equivalent or the complex envelope. The required sampling rate then only depends on the bandwidth of the modulated signal.
III. SystemC AMS Simulations: Speed Vs. Accuracy Tradeoff
The introduction of these AMS abstraction methods, which are facilitated by the models of computation of the SystemC AMS extensions, addresses the need to significantly improve simulation speed and efficiency of the AMS descriptions. This marks the beginning of a new era in which AMS and digital HW/SW systems can finally be simulated together.
In terms of simulation accuracy, the objective is to capture basic functionality relevant for the intended use case and to validate this against the specification, including AMS behavior. As these AMS system aspects are evaluated as part of a virtual prototype that uses a high-level (e.g., TLM) description of the digital HW/SW system, it is not expected that analog physical effects (e.g., parasitics and substrate noise) should become part of the AMS system model. Instead, dynamic linear and static non-linear behavior related to amplification, mixing, filtering, and so on of analog signals can be captured quite naturally and easily, without having a major impact on the simulation performance.
To enable inclusion of AMS descriptions in virtual prototypes, simulation speed should be comparable to the simulation performance when using TLM. Note that the abstraction and associated accuracy for the AMS description at the system level and circuit level are completely different, because different use cases are served and thus a true one-to-one comparison of the results cannot be given. This being said, Figure 2 gives first-order indications toward selection of the most applicable modeling strategy and modeling language.
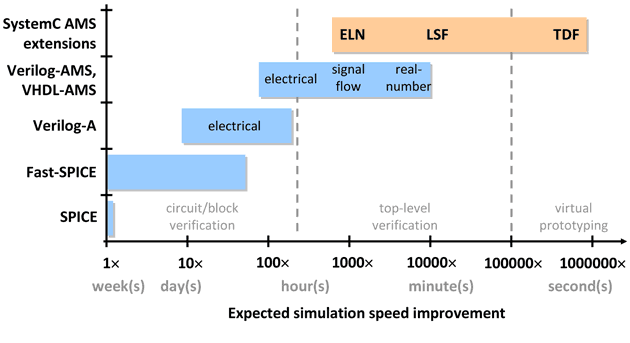
Figure 2: Expected simulation speed for different modeling languages compared to SPICE simulation.
Fast-SPICE solutions available in the market today show an improvement of a factor of 5-50 (compared to SPICE) and thus are very valuable for circuit/block verification. The simulation speed improvement offered by Fast-SPICE solutions makes them unsuitable for integration into a virtual prototype. The use of conventional AMS behavioral modeling techniques (e.g., Verilog-A, Verilog-AMS, and VHDL-AMS) including real-number modeling is beneficial for top-level verification, bringing a simulation speed improvement between 100 and 10,000. However, this is still not sufficient for virtual prototyping (e.g., to boot an operating system and to control a software-defined radio baseband processor and analog front-end).
The TDF model of computation offered by the SystemC AMS extensions facilitates a very efficient simulation approach, as TDF models are processed at discrete time points without using the dynamic scheduling of the discrete-event kernel of SystemC. This makes TDF the most powerful modeling style for the creation of AMS descriptions in virtual prototypes.
For a wireline communication system [3], a Fast-SPICE simulation for the analog front-end takes approximately 15 hours to simulate 1ms of real time. By creating an abstracted description using the SystemC AMS extensions, the simulation takes 1.5 hours to simulate 1 second of real time. Although a true comparison cannot be made because a different abstraction and accuracy have been applied, the values show a ratio of 10,000 in simulation speed.
In the case of applying baseband modeling, a dedicated data type is defined as a specialized class to store the complex envelope for the individual carrier frequencies. This abstraction method is applied with success in a case study presented at the DATE Conference 2010 [4]. The simulation results show that the transient simulation up to a bandwidth of 2.4 GHz for the transmission of 1,000 bits takes 63 seconds. When replacing the signal type double with the specialized data type for baseband modeling, the simulation bandwidth is reduced according to the bandwidth of the complex envelope, resulting in a simulation time of 36ms. This brings a speed improvement of a factor of 1,750.
IV. SystemC AMS Standard: A Bright Future
After the release of the AMS 1.0 standard, the OSCI AMS working group has continued to promote the use of the SystemC AMS extensions. In addition, they will further advance the AMS standard, addressing additional important topics as defined in the AMS requirements specification [2].
In order to get started with the SystemC AMS extensions, please visit the AMS Working Group page [5] to find more information on the released SystemC AMS standard and industry support. The SystemC AMS User's Guide [2] is part of the standard and offers a good starting point for exploring the capabilities of this new modeling language. The User's Guide will further explain the modeling fundamentals and abstraction methods as presented in this paper, and also offers many code and application examples.
We encourage the SystemC and AMS community to learn more about the simulation power and speed offered by the SystemC AMS extensions. And, if you need some guidance in this journey, feel free to contact us via the AMS forum.
V. Acknowledgments
The author wishes to thank Karsten Einwich of Fraunhofer IIS/EAS Dresden, Gerhard Nössing of Lantiq Austria GmbH, and François Pecheux of the Université Pierre et Marie Curie in Paris for sharing their simulation benchmark results using the SystemC AMS extensions.
VI. References
[1] C. Grimm, M. Barnasconi, A. Vachoux and K. Einwich, "An Introduction to Modeling Embedded Analog/Mixed-Signal Systems Using SystemC AMS Extensions," Open SystemC Initiative, June 2008.
[2] SystemC AMS 1.0 Standard, including AMS Language Reference Manual, User's Guide, and requirements specification
[3] K. Einwich, C. Grimm, M. Barnasconi and A. Vachoux, "Introduction to the SystemC AMS DRAFT Standard", embedded tutorial, Proc. IEEE Intl. SOC Conf., 2009.
[4] K. Einwich, C. Grimm, F. Pecheux, and M. Barnasconi, "Application of the SystemC AMS Standard", tutorial, Proc. DATE Conference, 2010.
Originally published as a DAC Knowledge Center Article.
This material is protected under the copyright laws of the U.S. and other countries and any uses not in conformity with the copyright laws are prohibited. Copyright for this document is held by the creator—authors and sponsoring organizations—of the material, all rights reserved.

Martin Barnasconi is the AMS Working Group Chairman, OSCI, and Product Manager AMS/RF System Design Methods, NXP Semiconductors, The Netherlands.

